|
Let the real symmetric matrix A
have order n × n.
We shall prove (i) by induction on n, the order
of matrix.
For n = 1,
the theorem is obvious, as it is a diagonal matrix. Let us assume
that the theorem
holds for all symmetric matrices of order ( n - 1 )
× ( n - 1 ) . Let A be
symmetric of order n × n.
Since A has at least one eigenvalue ( by theorem 10.2.1 ),
let it be called
 .
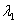Let
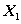be a unit
eigenvector for this eigenvalue, i.e., ||
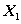|| = 1 and A
=
.
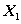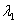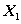We construct an orthonormal
basis (using Gram Schmidt process )
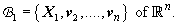
let
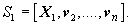
Note that
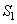 is
an orthonormal matrix, i.e.,
 .
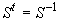Consider the matrix
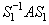 .We
have
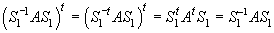
Thus,
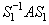is an symmetric matrix and its first column is given by
()(
)
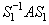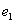where
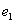is
the standard unit vector in
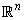 ,first
component 1and all other components zero, since
=
,
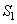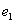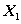we have
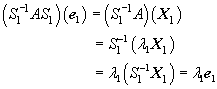
Hence, we can write
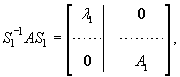
where
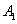 is
a ( n - 1 )
× ( n - 1 ) symmetric matrix
. By induction hypothesis, there exists a
( n - 1 )
× ( n - 1 ) orthogonal
matrix
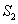such that
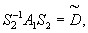 a
( n - 1 )
× ( n - 1 )
diagonal matrix. Let
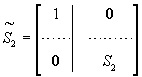
Then,
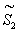 is
a ( n × n )
orthogonal matrix . Further
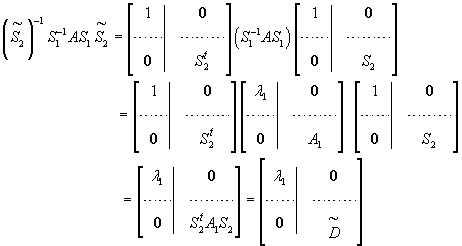
Thus, if we put
P :=
,
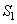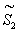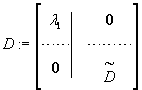
Then P is an orthogonal matrix, D is a diagonal
matrix with
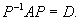
This proves (i), (ii) and (ii) follows as in theorem 10.1.2. .
|
AP
= D , a diagonal matrix.